이전 글에서 DQ변환은 두번 이루어진다교 했었죠.
그리고 Clarke 변환에 대해서 다루었었습니다. 아래 링크 첨부해요.
DQ변환. 그래 공식은 알겠는데 이게 무슨 의미야? + clarke 변환
주의!!) 이번 글은 이해하기 위해서 간단한 선형대수학(좌표변환 행렬)과 전기기기(유도기, 동기기)에 대한 선행지식이 필요합니다. 핵심요약은 가장 밑에 있습니다.https://www.youtube.com/watch?v=vdeVVT
nowrang.tistory.com
우리는 Clarke 변환을 통해서 120도 간격으로 위치하던 UVW(또는 ABC) 3상을 90도 간격으로 직교하는
알파와 베타 축으로 좌표변환을 이뤄냈습니다.

그러나 그렇게 좌표변환해서 본 알파, 베타 축 전류들은 여전히 교류 파형이었죠.
DQ변환의 목적은 선형화와 DC화 였으니 아직 한 단계가 더 남았습니다.
Park 변환은 당연하지만 Park라는 분이 제안한 변환 방식입니다.
단순합니다. 좌표계를 회전시키는 거죠. 회전 행렬을 곱하면 좌표계가 회전을 하는 것처럼 계산됩니다.
아래 그림을 참고해주세요.
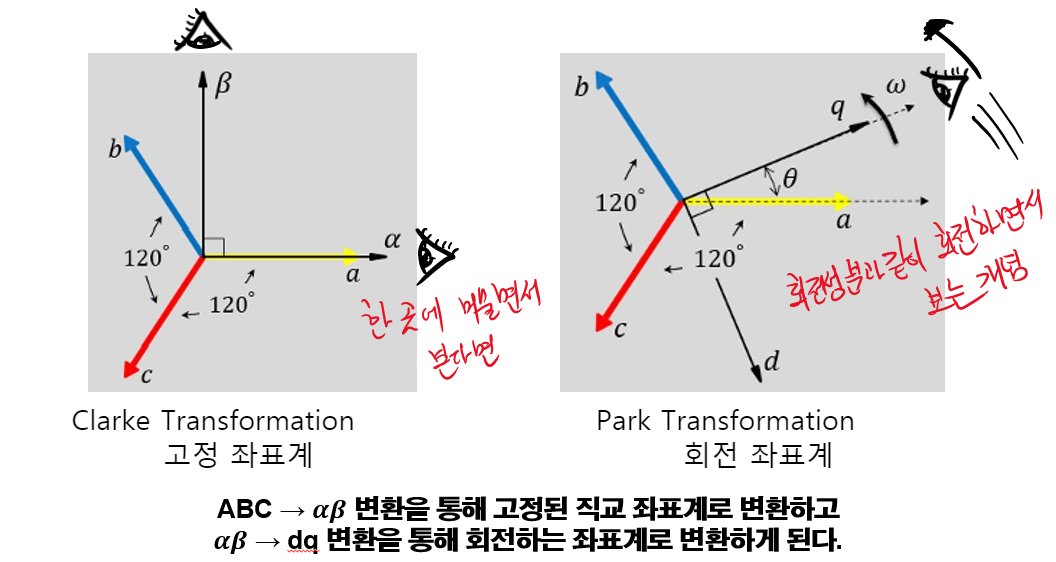
이렇게 Clarke 변환한 알파베타 고정좌표계에서는 눈이 한 곳에 머물면서 벡터가 돌아가는 것을 보고 있었다면,
Park 변환한 회전좌표계에서는 눈이 회전하는 dq 회전 좌표계의 d축과 q축에 딱 붙어서 회전을 하는 것처럼 봅니다.
어떻게 이게 가능하냐면, 회전 변환 행렬에 보통 넣어주는 회전 값인 Theta 값을 각속도와 시간의 함수로 넣어주면 됩니다.

위 그림이 회전 행렬을 적용한 예시입니다.
theta 만큼 반시계로 회전한 점의 위치를 찾으려면, 원래 위치에 저런 회전 변환 행렬을 곱해주면 되죠.
그런데 만약에 theta 대신에 wt를 넣어준다면? (w는 각속도, t는 시간입니다)
w의 각속도로 회전하게 되겠죠?
그런데 그 속도를 회전하는 자기장 벡터와 같은 속도로 맞춰준다면? 즉, 전류의 주파수랑 똑같이 맞춘다면?
좌표계가 회전하는 속도가 벡터가 회전하는 속도랑 똑같아지죠.
그러면 좌표계에서 바라봐도 멀어졌다 가까워졌다 하지않고 일정한 거리에 있으니 일정한 값으로 보이게 됩니다.

이제 clarke 변환 * park 변환을 미리 곱해둔 변환행렬은 이렇습니다.

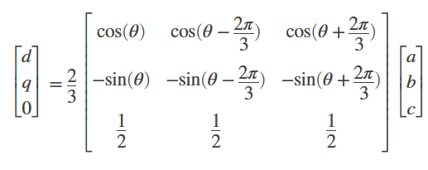
그런데 말입니다.
우리가 속도는 전류 주파수에 맞춘다고 해도, 거기에다가 플러스로 임의의 theta를 더해주면 dq좌표계의
d축 위치를 조정할 수 있지 않습니까?
보통 동기기에서는 회전자의 d축에 dq좌표계의 d축이 일치하도록 정렬을 해줘야 합니다.
유도기가 되면 보이지 않는 공극자속밀도의 d축 위치를 전압방정식과 자속방정식 등으로 추정해서 맞춰져야 하죠.
유도기는 어디가 d축이라고 정해져 있지 않고, 부하와 속도에 따라서 계속 바뀌잖아요. 이런 면에선 유도기의 벡터제어가 좀 어렵습니다.
'전기공학' 카테고리의 다른 글
| 모터의 극 수에 따른 장점과 단점. (0) | 2020.12.25 |
|---|---|
| 모터는 3상이 끝일까? 다상 모터의 장단점들 (8) | 2020.11.19 |
| 전력전자 회로에 쓸만한 고 전압센서 회로 예제(feat. AMC1301) (0) | 2020.11.14 |
| 전기전자에서 말하는 DC 오프셋 Offset 은 무슨 의미일까? (0) | 2020.11.14 |
| orCAD, EAGLE, Ki-CAD 풋프린트, 심볼 라이브러리 사이트 (0) | 2020.11.10 |



